حساب وقت الشروق (Sunrise) والغروب (Sunset)

حساب وقت الشروق (Sunrise) والغروب (Sunset)
مقدمة
يُعتبر حساب وقت الشروق (Sunrise) والغروب (Sunset) من الركائز الأساسية في علم الفلك البحري (Nautical Astronomy)، إذ يعتمد عليه الملاحون لتحديد موقع السفينة، وضبط الجداول الزمنية، وتنظيم المراقبة الليلية والنهارية. ورغم التطور الكبير في الأجهزة الإلكترونية الحديثة، ما زالت الطريقة الفلكية البحرية تُدرّس وتُستخدم كخطة بديلة عند تعطل الأنظمة الإلكترونية.
التعريفات الأساسية
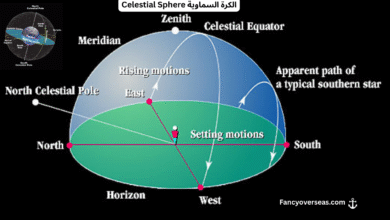
الشروق (Sunrise): اللحظة التي يظهر فيها الطرف العلوي لقرص الشمس فوق الأفق الشرقي.
الغروب (Sunset): اللحظة التي يختفي فيها الطرف العلوي لقرص الشمس تحت الأفق الغربي.
الارتفاع (Altitude): الزاوية بين جرم سماوي (الشمس) والأفق الظاهري، وتقاس بالدرجات.
خط العرض Latitude (φ): موقع المراقب شمالاً أو جنوباً بالنسبة لخط الاستواء.
الميل الشمسي Declination (δ): الموقع الزاوي للشمس شمالاً أو جنوباً عن خط الاستواء السماوي.
زاوية الساعة Hour Angle (H): الفرق بين خط الزوال المحلي (Local Meridian) وخط الزوال السماوي للشمس.
الأساس الفلكي لحساب الشروق والغروب
يعتمد تحديد لحظتي الشروق والغروب على العلاقة المثلثية بين:
خط العرض (φ) للموقع.
الميل الشمسي (δ) للشمس.
زاوية الساعة (H).
المعادلة الفلكية الأساسية:
\cos H = – \tan φ \cdot \tan δ
حيث:
H = زاوية الساعة عند لحظة الشروق أو الغروب.
φ = خط العرض.
δ = ميل الشمس (من الجداول الفلكية).
ومن هذه العلاقة يمكن حساب وقت الشروق والغروب كالآتي:
وقت\ الشروق = 12h – \frac{H}{15}
وقت\ الغروب = 12h + \frac{H}{15}
(حيث أن 15° تعادل ساعة واحدة زمنية).
خطوات حساب وقت الشروق والغروب فلكياً
- الحصول على البيانات الفلكية
الميل الشمسي (Declination) من الجداول الفلكية البحرية Nautical Almanac.
معادلة الزمن Equation of Time لتصحيح الزمن الشمسي الظاهري.
- تحديد موقع المراقب
معرفة خط العرض (Latitude φ) من تقدير الموقع أو من أجهزة GPS.
- حساب زاوية الساعة (H)
باستخدام المعادلة:
\cos H = – \tan φ \cdot \tan δ
- تحويل الزاوية إلى زمن
كل 15° = ساعة زمنية.
H/15 يعطي مقدار الزمن من الظهر الحقيقي (Local Apparent Noon) إلى الشروق أو الغروب.
- إضافة التصحيحات
الانكسار الجوي (Atmospheric Refraction): يؤثر على رؤية قرص الشمس، ويُحسب عادة بإضافة نصف قطر الشمس (≈ 16 دقيقة قوسية) + الانكسار (≈ 34 دقيقة قوسية).
معادلة الزمن (Equation of Time): لتصحيح الفارق بين الزمن الشمسي الظاهري والزمن المدني.
التوقيت الزمني المحلي (Local Time Zone): ضبط الزمن على المنطقة الزمنية.
مثال توضيحي مبسط
خط العرض: 30° شمالاً.
اليوم: 21 مارس (الاعتدال الربيعي).
ميل الشمس (δ) ≈ 0°.
المعادلة:
\cos H = – \tan 30 \cdot \tan 0 = 0
وبالتالي:
وقت الشروق = 12h – (90/15) = 12 – 6 = 6 صباحاً.
وقت الغروب = 12h + (90/15) = 12 + 6 = 6 مساءً.
وهذا يطابق الاعتدال حيث يتساوى الليل والنهار.
الطرق التقليدية والحديثة
- الطرق التقليدية
استخدام الجداول الفلكية البحرية Nautical Almanac.
الحساب المثلثي باستخدام القوانين الكروية.
استعمال السدس البحري (Sextant) لمراقبة ارتفاع الشمس وقت الأفق.
- الطرق الحديثة
أجهزة GPS وأنظمة ECDIS تعطي وقت الشروق والغروب أوتوماتيكياً.
تطبيقات الهاتف الذكي والبرامج الفلكية مثل Stellarium وSkySafari.
مع ذلك، يظل التعليم البحري يعتمد على الطريقة الفلكية التقليدية كبديل عند فشل الأجهزة.
الأهمية البحرية لحساب الشروق والغروب
- تحديد الموقع البحري: البحارة يستخدمون ارتفاع الشمس عند الشروق والغروب لتقدير خط الطول والعرض.
- تنظيم جداول المراقبة: تقسيم ساعات العمل بين الطاقم البحري يعتمد على النهار والليل.
- السلامة الملاحية: الرؤية تتغير عند الشروق والغروب، ما يتطلب رفع الأعلام أو تشغيل الأضواء الملاحية.
- الملاحة التقليدية: قبل اختراع GPS، كان الاعتماد على الفلك البحري أساسياً.
- الأنشطة البحرية الأخرى: مثل الصيد، الغوص، والرحلات السياحية التي تعتمد على توقيت الشروق والغروب.
الخاتمة
يمثل حساب وقت الشروق والغروب فلكياً أحد أقدم التطبيقات العملية لعلم الفلك في خدمة الملاحة البحرية. ورغم التطور التكنولوجي الهائل، يبقى هذا الحساب ذا أهمية تعليمية وعملية، إذ يوفر للملاحين وسيلة دقيقة لتحديد الزمن والموقع وضبط عمليات السفينة. إن الجمع بين الطرق التقليدية الحديثة يعكس مدى استمرارية الفلك البحري كأحد العلوم التي تربط الإنسان بالكون والبحر.
المصادر
- The Nautical Almanac, UK Hydrographic Office.
- Bowditch, American Practical Navigator.
- International Maritime Organization (IMO) – STCW Training Manuals.
- Meeus, Jean: Astronomical Algorithms.
- Astronomical Applications Department – U.S. Naval Observatory.